二項ロジスティック回帰
目次
二項ロジスティック回帰¶
import matplotlib.pyplot as plt
import numpy as np
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [1], in <cell line: 1>()
----> 1 import matplotlib.pyplot as plt
2 import numpy as np
ModuleNotFoundError: No module named 'matplotlib'
# 表示する文字サイズを調整
plt.rc("font", size=20)
plt.rc("legend", fontsize=16)
plt.rc("xtick", labelsize=14)
plt.rc("ytick", labelsize=14)
# 乱数
np.random.seed(777)
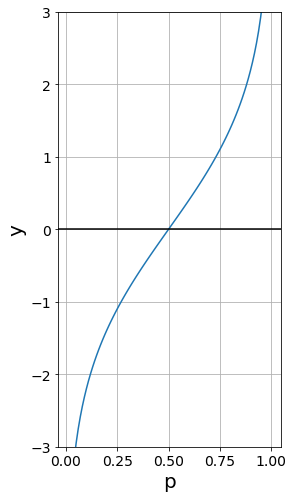
ロジット関数の可視化¶
fig = plt.figure(figsize=(4, 8))
p = np.linspace(0.01, 0.999, num=100)
y = np.log(p / (1 - p))
plt.plot(p, y)
plt.xlabel("p")
plt.ylabel("y")
plt.axhline(y=0, color="k")
plt.ylim(-3, 3)
plt.grid()
plt.show()
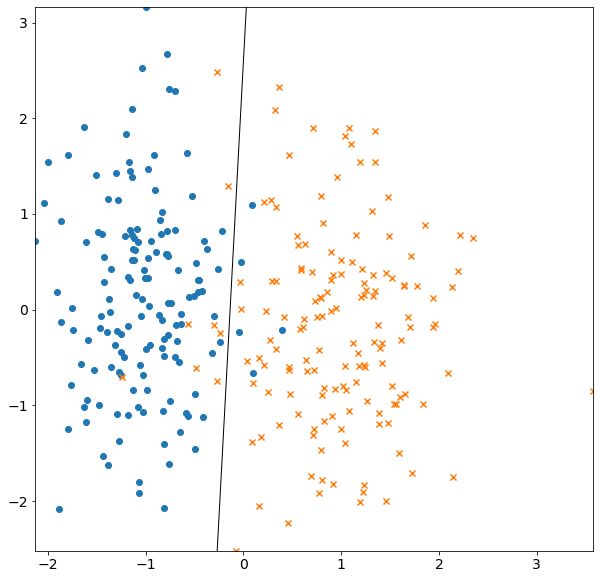
ロジスティック回帰¶
人工的に生成したデータに対してロジスティック回帰を実行します。
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
# データセット
X, Y = make_classification(
n_samples=300,
n_features=2,
n_redundant=0,
n_informative=1,
random_state=2,
n_clusters_per_class=1,
)
# ロジスティック回帰を学習
clf = LogisticRegression()
clf.fit(X, Y)
# 決定境界の直線を求める
b = clf.intercept_[0]
w1, w2 = clf.coef_.T
b_1 = -w1 / w2
b_0 = -b / w2
xmin, xmax = np.min(X[:, 0]), np.max(X[:, 0])
ymin, ymax = np.min(X[:, 1]), np.max(X[:, 1])
xd = np.array([xmin, xmax])
yd = b_1 * xd + b_0
# グラフを描画
plt.figure(figsize=(10, 10))
plt.plot(xd, yd, "k", lw=1, ls="-")
plt.scatter(*X[Y == 0].T, marker="o")
plt.scatter(*X[Y == 1].T, marker="x")
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.show()
警告
補足:max_iterの値が小さすぎる場合は警告がでます。
clf_warning = LogisticRegression(max_iter=2, solver="sag") clf_warning.fit(X, Y)
ConvergenceWarning: The max_iter was reached which means the coef_ did not converge

